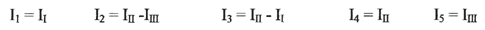При расчете цепи методом контурных токов выдвигаются два предположения:

• в каждом контуре протекают независимые друг от друга расчетные (контурные) токи;
• ток каждой ветви равен алгебраической сумме контурных токов, протекающих через эту ветвь.

Рассмотрим схему, представленную на рис. 5

При расчете рекомендуется следующая последовательность действий:

• находят в цепи ветви, узлы и контуры;
• указывают произвольные направления токов в ветвях и направления обхода контуров;
• произвольно выбирают направления контурных токов, обычно совпадающие с направлениями обхода контура;
• для независимых контуров составляют уравнения по второму закону Кирхгофа относительно неизвестных контурных токов I₁, I₁₁, I₁₁₁.

Для рассчитываемой электрической цепи система уравнений будет иметь вид:

• для контура acef: (R_I + r₀₁ + R₃) I_I – R₃ I_II =E₁
• для контура abc: -R₃ I_I + (R₂ + R₃ +R₄) I_II — R₂ I_III = -E₂
• для контура bdc: -R₃ I_II + (R₂ + R₅ +R₆) I_III = E₂

В рассматриваемом примере при составлении уравнений принято во внимание то, что вторая (R₂, E₂) и третья (R_з) ветви электрической цепи являются смежными и по ним протекают два контурных тока, каждый из которых обусловливает на резисторе смежной ветви падение напряжения, например, R₂I_II и R₂I_III (для токов второй ветви).

r₀₁ – внутреннее сопротивление источника ЭДС Е₁.

Токи в ветвях определяют алгебраическим суммированием контурных токов, протекающих через ту или иную ветвь. Контурный ток берется со знаком «плюс», если его направление совпадает с направлением тока ветви, и со знаком «минус» — при встречном направлении.