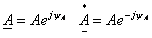Расчет производится с использованием тех же методов, что и цепей постоянного тока (отличие заключается в использовании комплексных чисел).
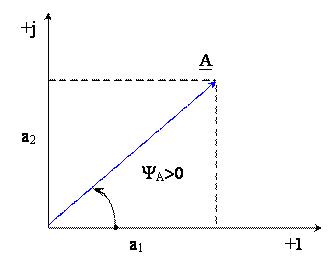
Любому вектору A, расположенному на комплексной плоскости, однозначно соответствует комплексное число, которое может быть записано в трех формах: алгебраической, тригонометрической и показательной.
В электротехнике, в отличие от математики, мнимую единицу обозначают j, так как буква i принята для обозначения мгновенного значения тока.
Алгебраическая форма записи комплексного числа:
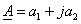
где а1— проекция вектора на ось действительных чисел (+1,Re);
а2— проекция вектора на ось мнимых чисел (+j,Jm).
Тригонометрическая формула записи
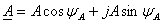
где А – длина вектора;
ΨA — угол наклона вектора к оси действительных чисел.
Показательная форма записи
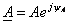
где А – модуль комплексного числа (соответствует действующему значению синусоидальной функции или длине вектора);
ΨA — аргумент комплексного числа (соответствует углу наклона вектора к оси действительных чисел или начальной фазе синусоидальной функции);
е – основание натурального логарифма е=2,718.
Если аргумент комплексного числа положительный, то угол откладывается в направлении движения часовой стрелки, если отрицательный – по часовой стрелке. Комплексные числа называют сопряженными, если их модули равны, а аргументы равны и противоположны по знаку